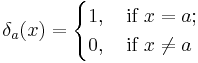Free module
In mathematics, a free module is a free object in a category of modules. Given a set  , a free module on
, a free module on  is a free module with basis
is a free module with basis  .
.
Every vector space is free,[1] and the free vector space on a set is a special case of a free module on a set.
Contents |
Definition
A free module is a module with a basis:[2] a linearly independent generating set.
For an  -module
-module  , the set
, the set 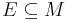 is a basis for
is a basis for  if:
if:
 is a generating set for
is a generating set for  ; that is to say, every element of
; that is to say, every element of  is a finite sum of elements of
is a finite sum of elements of  multiplied by coefficients in
multiplied by coefficients in  ;
; is linearly independent, that is, if
is linearly independent, that is, if  for
for 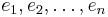 distinct elements of
distinct elements of  , then
, then  (where
(where 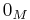 is the zero element of
is the zero element of  and
and 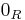 is the zero element of
is the zero element of  ).
).
If  has invariant basis number, then by definition any two bases have the same cardinality. The cardinality of any (and therefore every) basis is called the rank of the free module
has invariant basis number, then by definition any two bases have the same cardinality. The cardinality of any (and therefore every) basis is called the rank of the free module  , and
, and  is said to be free of rank n, or simply free of finite rank if the cardinality is finite.
is said to be free of rank n, or simply free of finite rank if the cardinality is finite.
Note that an immediate corollary of (2) is that the coefficients in (1) are unique for each  .
.
The definition of an infinite free basis is similar, except that  will have infinitely many elements. However the sum must still be finite, and thus for any particular
will have infinitely many elements. However the sum must still be finite, and thus for any particular  only finitely many of the elements of
only finitely many of the elements of  are involved.
are involved.
In the case of an infinite basis, the rank of  is the cardinality of
is the cardinality of  .
.
Construction
Given a set  , we can construct a free
, we can construct a free  -module over
-module over  . The module is simply the direct sum of
. The module is simply the direct sum of 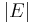 copies of
copies of  , often denoted
, often denoted 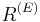 . We give a concrete realization of this direct sum, denoted by
. We give a concrete realization of this direct sum, denoted by 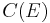 , as follows:
, as follows:
- Carrier:
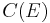 contains the functions
contains the functions 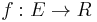 such that
such that 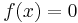 for cofinitely many (all but finitely many)
for cofinitely many (all but finitely many) 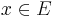 .
. - Addition: for two elements
 , we define
, we define 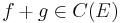 by
by 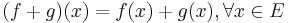 .
. - Inverse: for
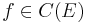 , we define
, we define 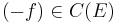 by
by 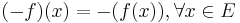 .
. - Scalar multiplication: for
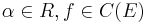 , we define
, we define 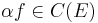 by
by 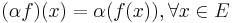 .
.
A basis for 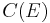 is given by the set
is given by the set 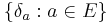 where
where
(a variant of the Kronecker delta and a particular case of the indicator function, for the set 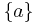 ).
).
Define the mapping 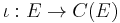 by
by 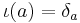 . This mapping gives a bijection between
. This mapping gives a bijection between  and the basis vectors
and the basis vectors 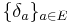 . We can thus identify these sets. Thus
. We can thus identify these sets. Thus  may be considered as a linearly independent basis for
may be considered as a linearly independent basis for 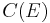 .
.
Universal property
The mapping 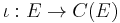 defined above is universal in the following sense. If there is an arbitrary
defined above is universal in the following sense. If there is an arbitrary  -module
-module  and an arbitrary mapping
and an arbitrary mapping 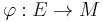 , then there exists a unique module homomorphism
, then there exists a unique module homomorphism 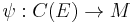 such that
such that 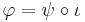 .
.
See also
Notes
References
- Iain T. Adamson (1972). Elementary rings and modules. University Mathematical Texts. Oliver and Boyd. pp. 65–66. ISBN 0-05-002192-3.
- Keown, R. (1975). An introduction to group representation theory. Mathematics in science and engineering. 116. Academic Press. ISBN 9780124042506.
- Hazewinkel, Michiel (1989). Encyclopaedia of mathematics: an updated and annotated translation of the Soviet "Mathematical encyclopaedia". Encyclopaedia of Mathematics. 4. Springer. ISBN 9781556080036.
External links
This article incorporates material from free vector space over a set on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.